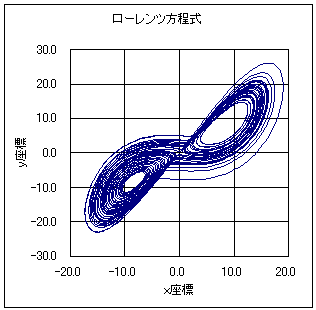
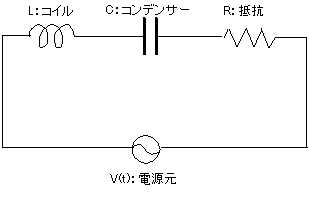
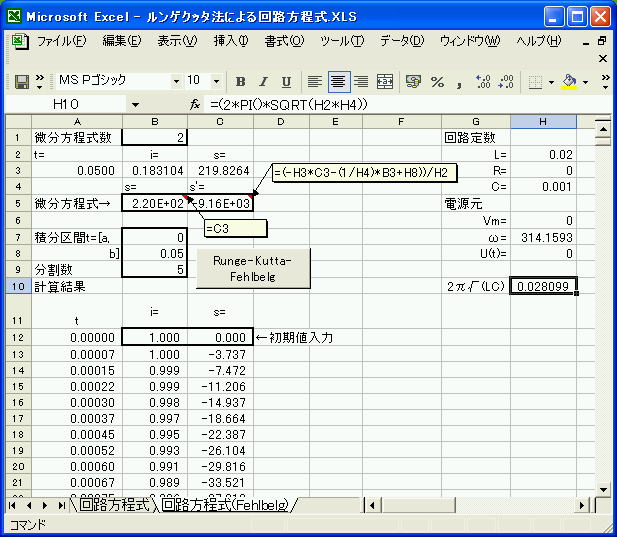
数値解析においてルンゲ=クッタ=フェールベルグ法 (Runge-Kutta-Fehlberg method) は、常微分方程式の数値解法であるルンゲ=クッタ法の一つである。特にルンゲ=クッタ=フェールベルグ法は、より高次なドルマン=プリンス法やキャッシュ=カープ法(英語)と同様に、時間の刻み幅を適用的に変化させることで、数値解法を安定させる手法である。4次の手法だが5次精度を実現できるという特徴を持つ。
出典
関連文献
- Simos, T. E. (1993). A Runge-Kutta Fehlberg method with phase-lag of order infinity for initial-value problems with oscillating solution. Computers & Mathematics with Applications, 25(6), 95-101.
- Handapangoda, C. C., Premaratne, M., Yeo, L., & Friend, J. (2008). Laguerre Runge-Kutta-Fehlberg Method for Simulating Laser Pulse Propagation in Biological Tissue. IEEE Journal of Selected Topics in Quantum Electronics, 14(1), 105-112.
- Paul, S., Mondal, S. P., & Bhattacharya, P. (2016). Numerical solution of Lotka Volterra prey predator model by using Runge–Kutta–Fehlberg method and Laplace Adomian decomposition method. Alexandria Engineering Journal, 55(1), 613-617.
- Filiz, A. (2014). Numerical solution of linear Volterra integro-differential equation using Runge-Kutta-Fehlberg method. Applied and Computational Mathematics, 3(1), 9-14.
- Simos, T. E. (1995). Modified Runge-Kutta-Fehlberg methods for periodic initial-value problems. Japan journal of industrial and applied mathematics, 12(1), 109.
- Seen, W. M., Gobithaasan, R. U., & Miura, K. T. (2014, July). GPU acceleration of Runge Kutta-Fehlberg and its comparison with Dormand-Prince method. In AIP Conference Proceedings (Vol. 1605, No. 1, pp. 16-21). AIP.
外部リンク
- Runge-Kutta-Fehlberg法による数値解析
関連項目
- ルンゲ=クッタ法
- ルンゲ=クッタ法のリスト
- キャッシュ=カープ法 (英語)
- ドルマン=プリンス法