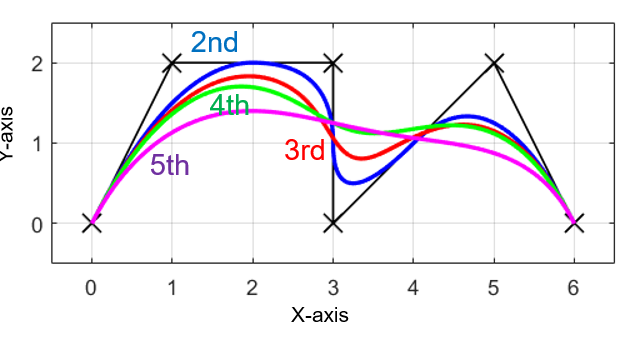
Kochanek–Bartelsスプライン曲線

Kochanek-BartelsスプラインまたはKochanek-Bartels曲線は、接線の動作を変更するために定義されたtension、bias、およびcontinuityパラメータを持つ3次エルミートスプラインである。

n 1ノットが与えられると、

p ₀ 、...、 p _n 、

をn個の三次エルミート曲線セグメントで補間する。各曲線には、開始接線d_iと終了接線d_{i 1}で定義される開始点p_i と終了点 p_{i 1}がある。

${\displaystyle \mathbf {d} _{i}={\frac {(1-t)(1 b)(1 c)}{2}}(\mathbf {p} _{i}-\mathbf {p} _{i-1}) {\frac {(1-t)(1-b)(1-c)}{2}}(\mathbf {p} _{i 1}-\mathbf {p} _{i})}$

${\displaystyle \mathbf {d} _{i 1}={\frac {(1-t)(1 b)(1-c)}{2}}(\mathbf {p} _{i 1}-\mathbf {p} _{i}) {\frac {(1-t)(1-b)(1 c)}{2}}(\mathbf {p} _{i 2}-\mathbf {p} _{i 1})}$

ここで、

各パラメータを0に設定すると、Catmull-Rom splineが得られる。

1996年のSteve Noskowiczのソースコードは、実際にこれらの値が描画されたカーブに与える影響を記述している。

コードには、これらのスプラインをBASICダイアレクトで生成するために必要なマトリックスサマリーが含まれている。

外部リンク

• Shane Aherne. “Kochanek and Bartels Splines”. Motion Capture — exploring the past, present and future. 2007年7月5日時点のオリジナルよりアーカイブ。2009年4月15日閲覧。

• Doris H. U. Kochanek, Richard H. Bartels. “Interpolating splines with local tension, continuity, and bias control”. SIGGRAPH '84 Proceedings of the 11th annual conference on Computer graphics and interactive techniques. ACM. pp. 33–41. 2014年9月23日閲覧。